
Mandelbrot
Il numero 206 de Le Scienze, dell'ottobre 1985, presentava in copertina questa sorprendente immagine:

Un'esplosione solare? La gemmazione di qualche improbabile microscopico organismo? No, era semplicemente la rappresentazione grafica di una porzione infinitesima dell'ormai celeberrimo insieme di Mandelbrot...
Per chi si diverte (come me...) a sprecare il proprio tempo sui giochini matematici, il magistrale articolo di A.K. Dewdney (e i tanti che seguirono sull'argomento) costituì una specie di rivelazione, che apriva una porta sul magico e misterioso mondo dei frattali. Non è difficile trovare decine e decine di riferimenti, in rete, sull'argomento; né è difficile trovare programmi migliori del mio, in seguito presentato, che consentano di esplorare i circumvoluti segreti dell'insieme. Però fu proprio grazie a (o per colpa di) questo tema che comprai il mio primo computer (un Commodore 128, dotato di ben 1 MHz di clock innalzabile a 2 MHz se si rinunciava alla grafica durante l'elaborazione...); e quindi mi fa piacere, quasi vent'anni dopo e dotato di un PC mille volte più potente, il proporre un programmino che alla fine mi soddisfa, essendo esso finalmente in grado di eguagliare la qualità delle immagini proposte da Dewdney. Come nei seguenti casi...
Nota: il programma produce immagini da 724 x 724 pixels, ampie 1,536 Mb: per non appesantire eccessivamente il download di questa pagina, quelle di seguito mostrate sono ridotte a 470 x 470 pixels e compresse in formato jpg. Di conseguenza, occupano 50-100 Kb ciascuna, ma sono di qualità e dimensioni inferiori rispetto alle originali.
 |
 |
 |
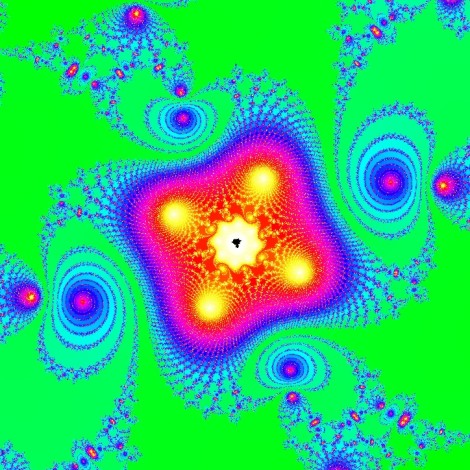 |
Cos'è realmente l'insieme di Mandelbrot? In realtà, nessuno dei pixel colorati delle immagini di cui sopra fa parte dell'insieme propriamente detto; l'insieme vero e proprio è costituito (quasi...) solo dalle parti in nero che si vedono apparire qui e là nelle immagini. Le affascinanti rappresentazioni colorate di cui sopra descrivono invece in qualche modo i punti che ambiscono senza riuscirvi a far parte dell'insieme...
Chi non sapesse cos'è l'insieme di
Mandelbrot e come esso (e i suoi dintorni) vengono rappresentati, può trovarne
una descrizione qui (Mandelbrot per principianti...).
![]()
Chi è già al corrente del tema,
può trovare le istruzioni per l'uso del programma fornito qui (Mandelbrot per
esperti...). ![]()
Il programma permette anche di rappresentare gli insiemi di Julia
connessi agli infiniti punti dell'insieme di Mandelbrot; una descrizione su come
generare tali insiemi col programma fornito può essere trovata qui.
![]()
Una piccola dissertazione sui criteri
di colorazione utilizzati dal programma viene fornita qui.
![]()
Scarica qui il programma Mandelbrot!
: il programma funziona con risoluzione 1024 x 768 pixel o superiore (ed almeno 65.536 colori); configurare lo schermo concordemente a tali indicazioni prima di eseguirlo.
Vai alla genealogia Torna a home page Invia informazioni Legge sulla privacy Copyrights ©